一、双目匹配步骤
双目匹配实际操作主要分为4个步骤:相机标定—图像校正—双目立体匹配—获取深度。
相机标定:
张氏相机标定法利用不同角度拍摄的多张棋盘图像,计算出相应的内参:$f_x, f_y, c_x, c_y$(内参),以及畸变系数$k_1,k_2,k_3,p_1,p_2$(径向畸变、切向畸变参数)。
在对内参进行标定时,我们已经得到两个相机的旋转矩阵和平移向量,再通过左右相机的内外参数,通过立体标定对左右两幅图像进行立体校准和对齐,最后确定两个相机的相对位置。
图像校正:
首先通过畸变系数进行畸变校正,径向畸变的校正公式为:
$x_c=x(1+k_1r^2+k_2r^4+k_3r^6)$
$y_c=y(1+k_1r^2+k_2r^4+k_3r^6)$
切向畸变的校正公式为:
$x_c=x+[2p_1y+p_2(r^2+2x^2)]$
$y_c=y+[2p_2x+p_1(r^2+2y^2)]$
然后进行立体校正,使得左右图像的成像原点坐标一致、两摄像头光轴平行、左右成像平面共面,这样一幅图像上任意像素点与其在另一幅图像上的对应点一定在同一行上,只需要对该行进行一维搜索即可匹配到对应点。
如下图,经过图像校正将两幅灰色图像校正为下侧共面的图像。
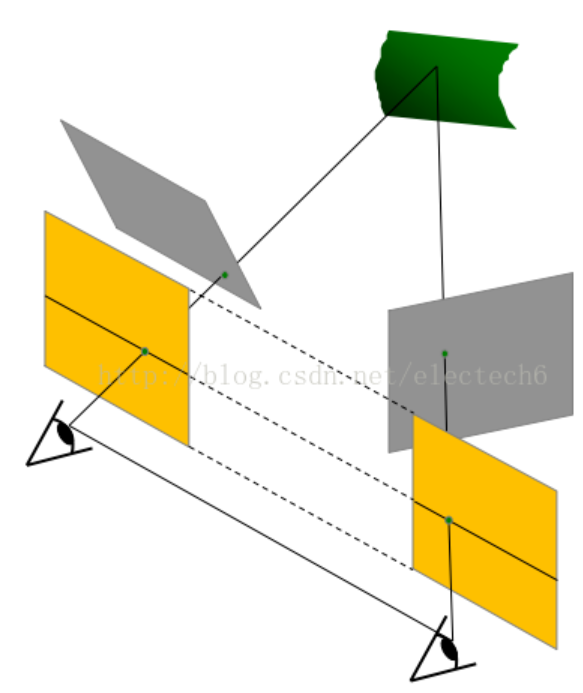
双目立体匹配:
双目立体匹配是把左右图像上对应的像素点匹配起来,得到视差图。
由于经过了立体校正后,匹配点是在同一行上的,所以可以在两张图的同一行中查找匹配点,通过匹配点得到每个点的视差d(下文提及)。
获取深度:
经过上面步骤的调整,我们找到了图像中对应点的参数,可以通过公式$z=\frac{b f}{d}$算出图像中各像素点所对应的深度信息,得到深度图。
公式$z=\frac{b f}{d}$的推导如下:
已知焦距为f,基线距离为b,左相机中所求像素点对于图像中心的偏移量$(xl,yl)$,右相机中对应像素点对于图像中心的偏移量$(xr,yr)$,我们需要求的是深度z,如下图:
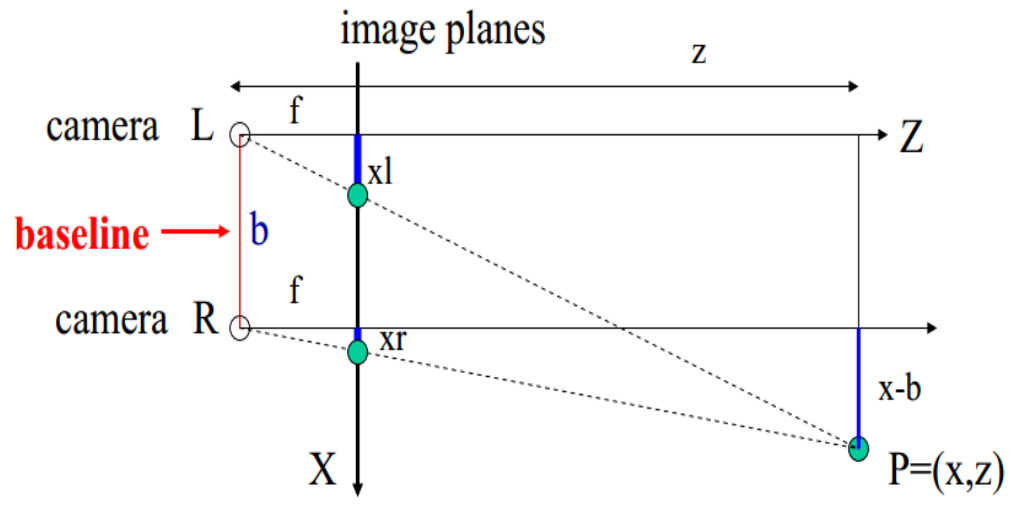
通过相似三角形的知识得到式子$z=f\times\frac{x}{xl},z=f\times\frac{x-b}{xr}$
有z、x两个未知量,由第一道式子有$x=\frac{z \cdot xl}{f}$
代入第二道式子:$z=f\times\frac{\frac{z \cdot xl}{f}-b}{xr}=\frac{z\cdot xl-bf}{xr}$
化简得$z=\frac{bf}{xl-xr}$
我们将xl-xr定义为视差d,则$z=\frac{bf}{d}$。
二、图像校正
1、畸变矫正
a、原理
通过摄像机将三维物体映射到二维图像中,是从世界坐标系到像素坐标系的映射过程。而因为透镜的成像原理,映射得到的图像会出现一定的畸变。(包括径向畸变和切向畸变)

对图像进行畸变矫正,即根据矫正原理和相机标定时得到的畸变参数,建立一个从原图像坐标到矫正后图像坐标的映射:$f(u,v)=(u_c,v_c)$
而由于摄影机成像时会有从实际图像坐标系到像素坐标系的转换$(x,y)→(u,v)$,矫正需要相对于图像坐标系,那么我们的矫正需要经过这样一个过程:
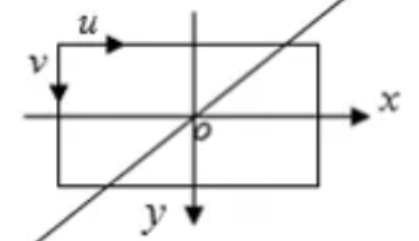
从图像坐标系到像素坐标系的映射公式比较简单,如下:
\(u=f_x·x+c_x\\
v=f_y·y+c_y\)
可以直接得到$h(u,v)=(x,y)$求出矫正前的$(x,y)$;
\(u_c=f_x·x_c+c_x\\
v_c=f_y·y_c+c_y\)
同理,矫正后的映射$g(x_c,y_c)=(u_c,v_c)$也直接利用上述公式得到。
接下来需要根据畸变矫正原理得到$f(x,y)=(x_c,y_c)$矫正的映射,分别处理径向畸变和切向畸变,公式如下:
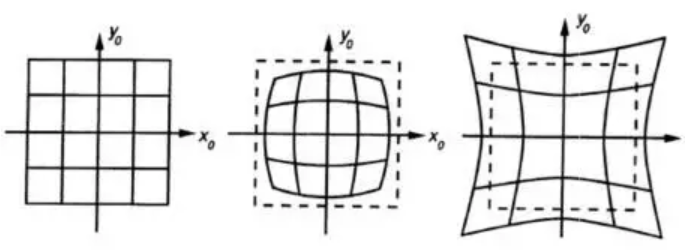
径向畸变:我们常用r=0(光心)处的泰勒级数展开的前几项来近似描述径向畸变。矫正径向畸变前后的坐标关系为:
$x_c=x(1+k_1r^2+k_2r^4+k_3r^6)$
$y_c=y(1+k_1r^2+k_2r^4+k_3r^6)$
$r^2=x^2+y^2$
切向畸变:切向畸变需要两个额外的畸变参数来描述,矫正前后的坐标关系为:
$x_c=x+[2p_1y+p_2(r^2+2x^2)]$
$y_c=y+[2p_2x+p_1(r^2+2y^2)]$
合并后得到:
$x_c=x(1+k_1r^2+k_2r^4+k_3r^6)+[2p_1y+p_2(r^2+2x^2)]$
$y_c=y(1+k_1r^2+k_2r^4+k_3r^6)+[2p_2x+p_1(r^2+2y^2)]$
$r^2=x^2+y^2$
这就是我们需要的映射$f(x,y)=(x_c,y_c)$。
由于存在畸变,畸变前坐标为整数,畸变后并不一定为整数。而在像素坐标系中,坐标都是整数,因此在这个过程中往往存在插值操作。(一般使用双线性插值的方法?)
b、OpenCV畸变矫正
OpenCV首先通过initUndistortRectifyMap()函数计算矫正映射。
void initUndistortRectifyMap(
InputArray cameraMatrix,
InputArray distCoeffs,
InputArray R,
InputArray newCameraMatrix,
Size size,
int m1type,
OutputArray map1,
OutputArray map2
);
其中最后三个变量m1type、map1、map2指定了矫正映射的类型。
《学习openCV3》里介绍了矫正映射的几种表示方法,不过我还不太理解这几个矫正映射和具体图像的对应关系。
- 双通道浮点数表示CV_32FC2:
映射由一个双通道浮点数NxM矩阵表示,矩阵中的每一个元素包含一个坐标,对应原图像中该像素坐标所对应矫正后图像像素坐标。在initUndistortRectifyMap()函数中通过map1表示。
若$map[2][3]=(4,5)$,则矫正后图像$(4,5)$上的像素点即为原图像中$(2,3)$上的像素点。(这个理解正确么?)
- 双矩阵浮点数表示CV_32FC1:
原理同上,不过由一个矩阵变成两个矩阵,一个矩阵对应X坐标,另一个矩阵对应Y坐标。在initUndistortRectifyMap()函数中通过map1、map2表示。
- 定点表示CV_16SC2:
映射由一个双通道有符号整数NxM矩阵表示,在initUndistortRectifyMap()函数中通过map1表示。
前面几个参数含义如下:
cameraMatrix:内参矩阵distCoeffs:畸变参数$k_1\ k_2\ p_1\ p_2\ (k_3 \dots)$,一般有4、5、8、12或14个元素。(不同数量的元素代表畸变矫正的精确度?)R:修正变换矩阵,不太理解它的作用。newCameraMatrix:新的内参矩阵。size:畸变矫正后图像大小。
得到矫正映射后,我们可以利用remap()函数将它们应用到实际图像中,在此过程中对坐标进行插值操作。
Void remap(
InputArray src,
OutputArray dst,
InputArray map1,
InputArray map2,
int interpolation,
int borderMode=BORDER_CONSTANT,
const Scalar&borderValue=Scalar()
);
各参数含义如下:
src:待矫正的原图像dst:经过矫正后的图像输出map1、map2:矫正映射interpolation:插值方式borderMode:边界插值类型borderValue:插值数值(?)
2、立体校正
a、原理
立体校正是为了使得左右图像的成像原点坐标一致、两摄像头光轴平行、左右成像平面共面,这样一幅图像上任意像素点与其在另一幅图像上的对应点一定在同一行上,只需要对该行进行一维搜索即可匹配到对应点。
如下图,经过立体校正将两幅灰色图像校正为下侧共面的图像。

经过标定,我们已经得到了两个图像平面对应的旋转矩阵和平移向量$(R,T) $,为了得到校正后图像,我们使用Bouguet校正算法。
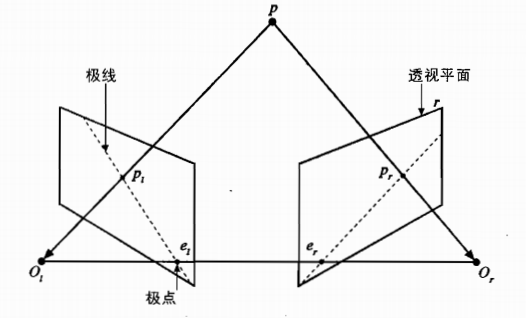
首先从几何关系上确定几个定义:
- 投影中心$O_r \ O_l$:两个摄像机透镜的中心
- 投影点$P_r \ P_l$:三维空间中的点P在图像平面中的投影位置。
- 极点$e_r \ e_l$:将两个投影中心相连,分别相交图像平面于极点。
- 极线$L_r \ L_l$:左右图像投影点和极点的连线。
- 极面:由两个投影中心/极点和实际点P所成平面。
当前两个图像平面的相对关系并不理想,但根据几何性质,我们可以得到:在左图像某一极线上的点所对应的点一定为右图像的对应极线上的某一点,以此可以仅在对应极线上进行一维搜索。
接下来使用Bouguet算法进行处理:
校正的第一步是使两个图像平面平行,可以根据旋转矩阵和平移向量$(R,T) $对其进行旋转操作,Bouguet算法将旋转矩阵R拆分成两个旋转矩阵$r_r \ r_l$,分别对两个图像平面进行旋转,此时两个图像平面达到平行,但是两图像的极线不平行。(大概理解如图)
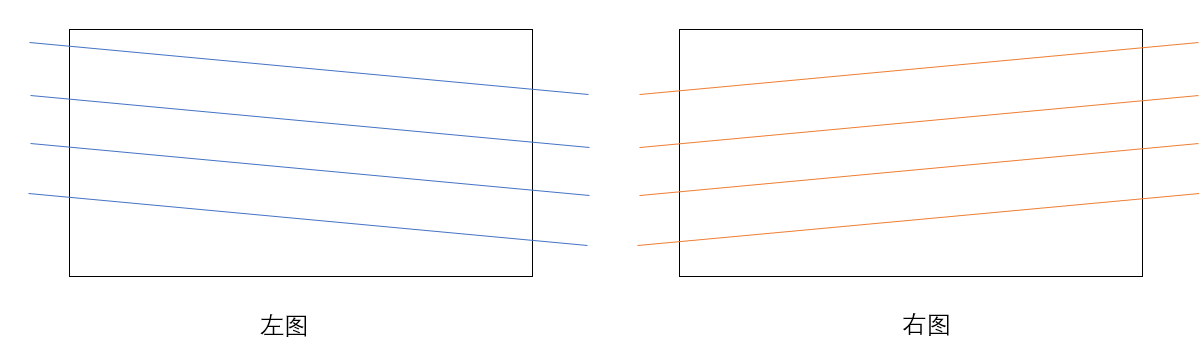
第二步是构造变换矩阵$R_{rect}$使得两图像的极线平行,此时利用了平移向量T,不过具体的数学运算暂时不太能理解,先把对应公式列出来。
\(e_1=\frac{T}{|T|} \\
e_2=\frac{[-T_yT_x0]^T}{\sqrt{T_x^2+T_y^2}} \\
e_3=e_1\times e_2 \\
R_{rect}=\begin{bmatrix}(e_1)^T \\ (e_3)^T \\ (e_3)^T \end{bmatrix}\)
经过第二步处理后的图像如下:
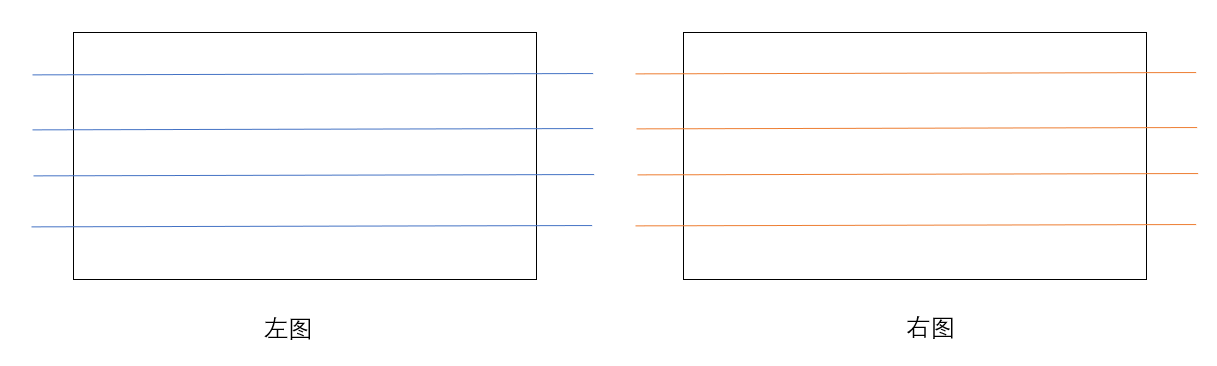
最后将旋转矩阵$r_r \ r_l$和变换矩阵$R_{rect}$进行合成,得到左右图像分别对应的总体变换矩阵(最终的映射关系?):
\(R_r=R_{rect}r_r\\
R_l=R_{rect}r_l\)
Bouguet算法的资料还提到了两个投影矩阵、一个重投影矩阵Q,还不太理解要如何应用它。
b、OpenCV立体校正
在OpenCV中,立体校正流程如下:
stereoRectify()函数实现Bouguet算法,得到立体校正参数。- 通过参数,利用
initUndistortRectifyMap()函数得到映射矩阵。 - 利用
remap()函数将它们应用到实际图像中,同时中对坐标进行插值操作。 - 对左右两张图像都进行以上操作,得到映射结果。
然后看一看stereoRectify()函数:
void stereoRectify(
InputArray cameraMatrix1,
InputArray distCoeffs1,
InputArray cameraMatrix2,
InputArray distCoeffs2,
Size imageSize,
InputArray R,
InputArray T,
OutputArray R1,
OutputArray R2,
OutputArray P1,
OutputArray P2,
OutputArray Q,
int flags=CALIB_ZERO_DISPARITY,
double alpha=-1,
Size newImageSize=Size(),
Rect* validPixROI1=0,
Rect* validPixROI2=0
);
各参数含义如下:
cameraMatrix1/cameraMatrix2:两个摄像机的内参矩阵distCoeffs1/distCoeffs1:两个摄像机的畸变参数imageSize:图像大小R、T:旋转矩阵和平移向量R1/R2:上述两个旋转矩阵$R_r \ R_l$P1/P2:上述两个投影矩阵$P_r \ P_l$Q:重投影矩阵alpha:拉伸参数,对图像进行拉伸?newImageSize:校正后的图像大小
得到的输出要作为initUndistortRectifyMap()函数的哪些参数输入?